[Algorithms] BFS : Breadth-First Search 너비우선탐색
Graph Algorithms
shortest-path problem(최단경로 문제)을 해결할 때 사용한다.
순서
- 문제를 그래프로 모형화
- 너비 우선탐색으로 문제 해결
그래프
연결 집합을 모형화한 것을 그래프라고 한다.
node와 edge로 이루어져 있다.
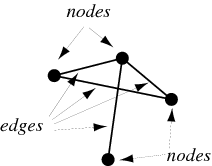
출처 : http://mathworld.wolfram.com/GraphEdge.html
너비우선탐색
개념
그래프 전체를 탐색하는 방법 중 하나이다. 너비우선탐색, 깊이우선탐색이 있다.
Facebook에서 연결되는 사람(촌) 중에 과자 회사에 다니고 있는 사람이 있는지 찾으려고 한다고 가정해보자.
A는 시작점인 '나'자신이고, B, C, D는 1촌, E, F, G, H는 2촌, I, J, K는 3촌이 된다. K가 과자 회사에 다닌다고 가정한다면 목표는 K가 된다.

시작점 A(나)에서 목표 K(과자회사에 다니는 사람)까지 도달하는 것을 기준으로 탐색을 한다.
시작점 A에서 갈 수 있는 후보를 확인한다. 이때 후보 탐색은 먼저 나와 닿아 있는 1촌에서 탐색해야 한다. 후보 : B, C, D
하나의 정점을 선택하는데, 이때 선택 기준은 후보 중 가장 먼저 추가된 것이다.
B, C, D 처럼 동일 시점에 생긴 경우 아무거나 선택해도 된다.
후보 정점은 FIFO(선입선출) 구조, 즉, Que 데이터 구조이다.
이제 1촌인 B로 이동하여 B의 1촌 중에 살펴본다. 즉, 후보가 될 수 있는 정점을 탐색한다. 후보 : E
마찬가지로 C로 이동하여 C에서 후보가 될 수 있는 점정를 탐색한다. 후보 : F, G
D로 이동하여 D에서 후보가 될 수 있는 정점을 탐색한다. 후보 : H
E, F, G, H가 있는 부분을 위와 같은 방법으로 탐색한다.
탐색은 목표인 K에 도달하거나 모든 탐색이 완료될 때까지 반복한다.
- 탐색 순서를 정리해 보면 아래와 같다.
A -> B, C, D
B -> E
C -> F, G
D -> H
E -> I
F
G
H -> J, K
I
J
K (목표 도달)
구현하기
관계를 표현하는 자료구조 Hash table로 그래프를 구현하고, Que를 이용하여 알고리즘을 구현한다.
그래프 구현하기
graph = {} # hash table 생성
graph["A"] = ['B', 'C', 'D'] # Key값 A에 Value로 B, C, D 넣음. 즉, A의 1촌 B, C, D가 조회된다.
graph["B"] = ["E"]
graph["C"] = ["F", "G"]
graph["D"] = ["H"]
graph["E"] = ["I"]
graph["F"] = []
graph["G"] = []
graph["H"] = ["J", "K"]
graph["I"] = []
graph["J"] = []
graph["K"] = []
알고리즘 구현하기
순서
- 비어 있는 queue를 준비
- 확인할 명단을 queue에 넣는다.
- queue에서 한사람씩 꺼내서 과자회사에 다니는 사람이 맞는지 확인한다.
- 맞으면 탐색 종료
- 과자회사에 다니는 사람이 없으면 이웃을 queue에 추가
다시 위 그래프로 생각해보면,

비어있는 queue srch = deque() 에 graph['A'] = ['B', 'C', 'D'] 가 들어간다. srch = graph['A']
'B'부터 한 사람씩 꺼내서 'pop('B')', 'B'=='과자회사 다니는 사람' 이 맞는지 확인한다.
맞느면 탐색을 종료하고, 아니면 'B'의 이웃'E'를 que에 추가한다.
'C','D'도 마찬가지 방법으로 탐색한다.
deque(double-ended queue)
Queue + Pop이 합쳐진 개념이다. 양쪽이 열려 있기 때문에, 양방향으로 push, pop이 가능하다.
즉, 크기가 가변적이다. 하지만 중간에 데이터를 삽입, 삭제하기 어렵다.
내가 짠 코드가 지저분해서 좀더 간결한 코드로 공부했다.
Python
# Program to print BFS traversal from a given source
# vertex. BFS(int s) traverses vertices reachable
# from s.
from collections import defaultdict
# This class represents a directed graph using adjacency
# list representation
class Graph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
# Function to print a BFS of graph
def BFS(self, s):
# Mark all the vertices as not visited
visited = [False]*(len(self.graph))
# Create a queue for BFS
queue = []
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
while queue:
# Dequeue a vertex from queue and print it
s = queue.pop(0)
print s,
# Get all adjacent vertices of the dequeued
# vertex s. If a adjacent has not been visited,
# then mark it visited and enqueue it
for i in self.graph[s]:
if visited[i] == False:
queue.append(i)
visited[i] = True
# Driver code
# Create a graph given in the above diagram
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print "Following is Breadth First Traversal (starting from vertex 2)"
g.BFS(2)
# This code is contributed by Neelam Yadav
# https://www.geeksforgeeks.org/breadth-first-traversal-for-a-graph/
JAVA
// Java program to print BFS traversal from a given source vertex.
// BFS(int s) traverses vertices reachable from s.
import java.io.*;
import java.util.*;
// This class represents a directed graph using adjacency list
// representation
class Graph
{
private int V; // No. of vertices
private LinkedList<Integer> adj[]; //Adjacency Lists
// Constructor
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
// Function to add an edge into the graph
void addEdge(int v,int w)
{
adj[v].add(w);
}
// prints BFS traversal from a given source s
void BFS(int s)
{
// Mark all the vertices as not visited(By default
// set as false)
boolean visited[] = new boolean[V];
// Create a queue for BFS
LinkedList<Integer> queue = new LinkedList<Integer>();
// Mark the current node as visited and enqueue it
visited[s]=true;
queue.add(s);
while (queue.size() != 0)
{
// Dequeue a vertex from queue and print it
s = queue.poll();
System.out.print(s+" ");
// Get all adjacent vertices of the dequeued vertex s
// If a adjacent has not been visited, then mark it
// visited and enqueue it
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext())
{
int n = i.next();
if (!visited[n])
{
visited[n] = true;
queue.add(n);
}
}
}
}
// Driver method to
public static void main(String args[])
{
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Breadth First Traversal "+
"(starting from vertex 2)");
g.BFS(2);
}
}
// This code is contributed by Aakash Hasija
참고문헌
[2] https://en.wikipedia.org/wiki/Breadth-first_search
[3] http://jpython.blogspot.kr/2012/12/bfs-algorithm-in-python.html
[4] https://www.geeksforgeeks.org/breadth-first-traversal-for-a-graph/
'Algorithms' 카테고리의 다른 글
| python3로 Circular Queue 구현하기 (0) | 2022.09.14 |
|---|---|
| [LeetCode] 9. Palindrome Number (0) | 2018.04.14 |
| [LeetCode] 1. Two Sum (0) | 2018.04.13 |